Chapter 4: Entering the Third Dimension

Chapter 4 Output

If you're learning OpenGL, it's very likely you're doing so to learn how to render three-dimensional data. In this chapter, we'll be placing our very first step in the world of three-dimensional computer graphics. We'll learn:

The mathematics used to describe transformations in a three-dimensional world
What coordinate systems are good for and how to use them
What polygon culling is and why it's used
How to render a rotating colored cube to the screen
Some new OpenGL function calls

As mentioned in the preface, you'll need some mathematical knowledge in order to understand some of the concepts presented, preferably knowledge of linear algebra. The mathematics in this chapter is as lightweight as possible without sacrificing the integrity of the presented concept.

Check the requirements before continuing

OpenGL 3.x / DirectX 10 Level Hardware

This chapter is 100% compatible with OpenGL 3.x level hardware by changing only a few lines of code.

Utilities

We use many of the functions from this chapter in the rest of the book, so let's create a few files that we can carry over from chapter to chapter. Please note that all of the functionality in this book is for demonstration purposes, and not optimized for performance. The functions provided here are verbose by design so that the flow of the code is easy to understand.

If you are looking for a professional-grade 3D mathematics library, you can find several excellent open source C++ libraries on the Internet or roll your own using high performance code. However, for this book, we're going to create a file called Utils.h, and add the following lines:

Now create a second file named Utils.c and insert the following lines:

Step-By-Step: Mathematics

If you're unfamiliar with the basics of linear algebra, much of the code in the listing from the previous section will seem like gibberish, and the rest of this chapter may be hard to follow. A few resources for learning linear algebra are listed in the chapter's conclusion. In the next sections, we'll explore what matrices are at a glance, how to use them in three-dimensional computer graphics, and how they are used in the code you've just copied.

You may ask yourself "how important is it to know all these calculations by heart?" For most of computer graphics, it is okay just to know the applications of the calculations since you'd store them in reusable functions. However, for complex computation, you would have to come up with calculations of your own using matrices, transformations, and other linear algebra.

The Matrix

A matrix is a mathematical construct that describes a grid (or array) of numbers composed of m row vectors and n column vectors. We use matrices to describe transformations from one coordinate space to another, such as rotation, scaling, translation, etc. In our programs, we use one type of matrix, namely the 4x4 square matrix (a matrix is square when n = m). Let's look at our 4x4 matrix M:

\( \mathbf{M} = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{bmatrix}\cdot \)

The notation used to access the single value stored in row 2, column 4 is:

\(M_{24} = 8\)

In a three-dimensional coordinate system such as ours, a 4x4 matrix contains the transformations for each axis in each column vector, which are the four horizontal columns that make up the matrix:

\( \mathbf{M} = \begin{bmatrix} Xx & Yx & Zx & Tx \\ Xy & Yy & Zy & Ty \\ Xz & Yz & Zz & Tz \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \)

The first three column vectors contain the x-, y-, and z-axes' transformations respectively, while the last column vector contains the translation, which we'll explore further below.

In our programs, we represent matrices with the structure Matrix, which contains an array of 16 floating-point elements, the total amount of elements in a 4x4 matrix. All of the matrix operations in Utils.h operate on this structure.

Matrix Multiplication

Before we continue with the explanation of how these transformations work, make sure that you fully understand matrix multiplication since we'll use it many times in this chapter by using the MultiplyMatrices function from the files that we've just created. Matrix multiplication is very important since it allows us to transform points from one coordinate system to another.

To understand how matrix multiplication works, let's take the following 2x2 matrices for simplicity's sake, which we'll name A and B:

\( \begin{aligned} \mathbf{A} = \begin{bmatrix} 1 & 2 \\\\ 3 & 4 \end{bmatrix}\cdot \\\\ \mathbf{B} = \begin{bmatrix} 5 & 6 \\\\ 7 & 8 \end{bmatrix}\cdot \end{aligned} \)

In order to get the product of A and B, which we'll name matrix C, we'll have to multiply each row vector in matrix A with each column vector in matrix B.

This means that if we wish to find the value to go into \(C_{11}\), we'll have to perform the following calculation:

\(C_{11} = A_{11}B_{11} + A_{12}B_{21} = 1\cdot5 + 2\cdot7 = 5+14 = 19\)

This is the same as the dot product of the first row vector of matrix A and the first column vector of matrix B. We repeat this process for the entire matrix, resulting in the following calculation for the 2x2 matrices:

\( \mathbf{C} = \begin{bmatrix} (A_{11}B_{11}+A_{12}B_{21}) & (A_{11}B_{12}+A_{12}B_{22}) \\\\ (A_{21}B_{11}+A_{22}B_{21}) & (A_{21}B_{12}+A_{22}B_{22}) \end{bmatrix} = \begin{bmatrix} 19 & 22 \\\\ 43 & 50 \end{bmatrix} \cdot \)

If we had used a 4x4 matrix multiplication instead of the above 2x2, the calculation would be much more extensive and best handled by a computer unless you enjoy multiplying matrices by hand. Note that matrix multiplication is not commutative, meaning that AB is not BA except when either A or B is an identity matrix (described below).

Our MultiplyMatrices function multiplies matrices m1, the multiplier, and m2, the multiplicand, and returns the product as a brand new matrix.

Identity Matrix

An important type of matrix is the identity matrix, which when multiplied by, produces the multiplicand. It is important because it serves as the basis for our transformations:

\( \mathbf{I} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \)

Identity matrices can only be formed from square matrices (m = n), and are visually distinguishable by a line of number ones along its main diagonal (which runs from top left to bottom right), whereas the rest of the matrix contains zeroes.

Another way of looking at an identity matrix is by the fact that it's composed of unit vectors. The column vector for x points in the x-direction, the column vector for y in the y-direction, the column vector for z in the z-direction, and the column vector used for translation set to zero for no translation.

Our own identity matrix is stored in the IDENTITY_MATRIX constant, declared as an extern in Utils.h and defined in the Utils.c file. If you browse through some of the functions in Utils.c, you'll notice that we use an identity matrix for almost every transformation.

Transformations

This brings us to the topic of transformations, which are an important tool in three-dimensional computer graphics. In fact, three-dimensional computer graphics would not be possible were it not for transformations. Transformations allow us to transform a point in space from one location to another using matrix multiplication. There are two transformation types used, affine transformations and projective transformations.

Affine transformations allow us to translate, rotate, scale, or shear our points in space relative to an origin using matrices. Most affine transformations do not alter the physical properties of an object, meaning that the distances from one point to another do no change.

Projective transformations on the other hand, transform points in order to "project" them onto a flat viewing plane, thus changing the properties of an object significantly. One example of such a projective transformation is the perspective projection matrix, which we will explore further on in this chapter.

Transformation Pipeline

Before we continue describing the various transformations in Utils.h, there's the important subject of coordinate systems. As you know, a coordinate system is a method used to describe the position of a point within a space, which in our case is three-dimensional. In computer graphics, we use several coordinate systems to transform our point to a displayable entity in a process called the transformation pipeline, let's take a quick look at each of its stages.

Object Space

The transformation pipeline starts in object space, which hosts an object's local coordinates, called object coordinates. These are the raw vertices provided by the modeling software, or as to relate it to the previous chapter, the points stored in the vertex buffer object.

World Space

To get the objects in a position relative to your world's origin, we transform its vertices using a modeling transform to bring them into world space. There could be several more steps for objects positioned relative to each other, also called modeling transforms.

Eye Space

Now that the object's position is relative to the world's origin, the next step is the view transform, which positions the world relative to the viewer's position, bringing the object into eye space. The viewer's position is the camera's position within the scene, but not the camera's function.

FYI: The Model-View Matrix Concept

Often in code samples, you'll notice something called a "model-view" transformation as a single step. This is because when you multiply matrices, transforms combine into a single matrix. While this practice is not wrong, and can actually save a tiny fraction of bandwidth, we don't use "model-view" matrices in this book to maintain proper coordinate system terminologies and avoid confusion.

Clip Space

The next step is to determine which vertices are actually viewable by the camera though a projection transformation after which the points are in clip space. We discuss the concept of viewing volumes and clipping at a later point in this chapter.

Normalized Device Space

The next step is to perform perspective division (or perspective projection), which brings our vertices into normalized device space. For OpenGL to be able to perform its rasterizing operations on the vertex data provided, the data needs to be in a two-dimensional format, along with a depth value for depth buffering.

Window Space

After the transformation to normalized device space, OpenGL takes over and feeds the vertex data into a process called rasterization, which generates fragments for the triangles, lines, and points that we described with our vertex information. At this point, OpenGL also applies the depth information to determine which fragments to discard due to overlap. After the composition of all the final fragments, the graphics hardware outputs the final image to the screen.

Translation Matrix

To move (or translate) a point from its origin, we must use what's called a translation matrix. The translation matrix stores the magnitude of the translation for each of the three dimensions in the last column vector of the 4x4 matrix:

\( \mathbf{T}=\begin{bmatrix} 1 & 0 & 0 & Tx \\ 0 & 1 & 0 & Ty \\ 0 & 0 & 1 & Tz \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \)

This matrix looks very similar to the identity matrix described earlier, with the exception of its last column vector. Multiplying by this matrix preserves rotation as well as scaling since the top left part of the matrix, where scaling and rotation values are stored, contains a 3x3 identity matrix.

Let's see how translation works, by translating the following point, represented as a column vector, three units along the y-axis:

\( \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 3 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 5 \\ 3 \\ 1 \end{bmatrix} \cdot \)

This operation is simple enough, and you can easily visualize how the y-component of the column vector increases its magnitude. This same principle applies to matrices when we wish to move an entire coordinate system instead of a single point:

\( \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 & 4\\ 2 & 3 & 4 & 1\\ 3 & 4 & 1 & 2\\ 4 & 1 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 3 & 4\\ 14 & 6 & 10 & 10\\ 3 & 4 & 1 & 2\\ 4 & 1 & 2 & 3 \end{bmatrix} \cdot \)

Notice how only the y-components of each column vector changes, since it's the only direction translated.

The function that we use to translate matrices is TranslateMatrix, which takes in a pointer to the matrix to translate, and x-, y-, and z-components that make up the translation stored in the translation column vector of the matrix.

Scaling Matrix

The matrix used for scaling transformations should look very familiar by now:

\( \mathbf{S}=\begin{bmatrix} Sx & 0 & 0 & 0 \\ 0 & Sy & 0 & 0 \\ 0 & 0 & Sz & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \)

This matrix looks remarkably similar to the identity matrix described earlier, only in this matrix the values on the main diagonal are scaling factors. This means that a scaling matrix with all of its scaling factors set to one is equal to an identity matrix, and will not change its multiplicand.

These scaling values may be positive for scaling outward (expansion), or negative for scaling inward (contraction). To scale in a single direction, simply set the directions you do not wish to scale to one (as with an identity matrix) and scale the remaining directions.

To scale an entire matrix by a factor of two in all directions, we would apply the following transformation:

\( \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 & 4\\ 2 & 3 & 4 & 1\\ 3 & 4 & 1 & 2\\ 4 & 1 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 2 & 4 & 6 & 8\\ 4 & 6 & 8 & 2\\ 6 & 8 & 2 & 4\\ 4 & 1 & 2 & 3 \end{bmatrix}\cdot \)

The function that we use to scale is ScaleMatrix, which takes in a pointer to the matrix to scale, and x-, y-, and z-components that define the scaling vector.

Rotation

To rotate, we use three separate matrices, each of which defines a rotation about the x-, y-, or z-axis, respectively. Let's look at the matrix required to rotate a point about its x-axis:

\( R_{x}(\theta)=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \)

If you look closely, you'll notice that this transformation does not affect the x-components of the column vectors or the x-column vector itself. This is because we rotate about an axis, visualized by rolling the axis of rotation between your fingers, so only the y- and z-vectors change direction:

Rotation about X

The same principle applies to the rotation about the y-axis:

\( R_{y}(\theta)=\begin{bmatrix} \cos\theta & 0 & \sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \)

Rotation about Y

As well as the z-axis:

\( R_{z}(\theta)=\begin{bmatrix} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \)

Rotation about Z

One thing to keep in mind when using rotation matrices is the order in which the rotations are applied to the point. A rotation about the x-axis followed by a rotation about the z-axis is not the same as a rotation about the z-axis followed by a rotation about the x-axis. Take for example the following matrix R:

\( \mathbf{R} = \begin{bmatrix} 5 & 0 & 0 & 0 \\ 0 & 6 & 0 & 0 \\ 0 & 0 & 7 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \)

When we rotate R 45-degrees about the y-axis, followed by a 90-degree rotation about the x-axis, the resulting matrix is:

\( \mathbf{R'} = \begin{bmatrix} 3.53 & -3.53 & 1.54 & 0 \\ 0 & 0 & -6 & 0 \\ 4.94 & 4.94 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \)

Whereas a 90-degree rotation about the x-axis followed by a 45-degree rotation about the y-axis would result in this matrix:

\( \mathbf{R'} = \begin{bmatrix} 3.53 & 0 & -3.53 & 0 \\ -4.24 & 0 & -4.24 & 0 \\ 0 & 7 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\cdot \)

We represent each of these rotational transformations with its own function in Utils.h: RotateAboutX, RotateAboutY, and RotateAboutZ, which all take in a pointer to the matrix to rotate as well as an angle of rotation in radians.

Projection Matrices

The last transformation we'll discuss is very different from the previously mentioned ones. Its purpose is to project points onto a two-dimensional plane instead of transforming points in a three-dimensional world. Because of this behavior, we call this type of matrix a projection matrix. There are two major types of projections used in three-dimensional computer graphics, namely orthogonal projection and perspective projection.

Orthogonal projection (also called parallel projection) doesn't apply foreshortening to lines, meaning that lines don't converge towards a point as in real life. With orthogonal projection, parallel lines will remain parallel, and will never intersect. This type of transformation is very useful in three-dimensional modeling programs where many objects at various distances display in a single viewport but require the same vertex transformations executed simultaneously.

Perspective projection on the other hand, mimics the real-life visual effect of foreshortening where objects at a distance appear smaller than objects nearby. This means that parallel lines will eventually intersect at a vanishing point, much like train tracks running off towards the horizon.

Perspective Projection

The function we use for perspective projection is CreateProjectionMatrix, which takes in the following parameters:

fovy, which represents the vertical field-of-view angle in radians, this is the angle between the top plane of the view frustum (see below) and the bottom plane
aspect_ratio, which is the ratio of width to the height of the viewport
near_plane, which is the distance from the eye to the near plane
far_plane, which is the distance from the eye to the far plane

If you've used OpenGL's fixed functionality, you'll probably recognize that this function is very similar to gluPerspective, and in fact, CreateProjectionMatrix mimics the behavior of this function exactly. We use this single matrix to convert the vertices from eye space to clip space as well as from clip space to normalized device space.

The parameters above describe a so-called viewing frustum (also called a viewing volume), used to determine which points to project onto the viewing plane:

Viewing Frustum

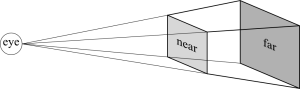
A frustum is a pyramid-like shape with its top cut off. The near and far planes have the same aspect ratio as your viewport. Because of this preservation of aspect ratio, your geometry will no longer look stretched when the window resizes as in the previous chapters. Projective transformation applies only to those points that fall within the viewing frustum, meaning that we clip the points that lie outside of the frustum.

To obtain normalized device coordinates, we map the entire viewing frustum to an axis-aligned cube measuring 2x2x2 units, located at the world's origin. This cube exists in order to facilitate the projection of the vertices onto the projection plane by OpenGL through parallel projection. After the vertices are in normalized device space, OpenGL is ready to use these points for rasterization.

FYI: Geometrical Concepts

When we speak of the viewing frustum and the normalized device coordinates cube, it's important to note that we don't generate actual geometry for these shapes. The planes of the frustum and the sides of the cube simply represent minimum and maximum boundaries for the vertices.

In most cases, you don't have to know the specifics of the projection matrix since the implementation rarely ever changes: simply define the code once and copy it into all of your projects. Until the OpenGL 3 version branch, the generation of the perspective projection matrix was part of OpenGL through the glFrustum function or GLU's gluPerspective.

To apply perspective projection transformations, we use the following matrix:

\( \mathbf{P}=\begin{bmatrix} xScale & 0 & 0 & 0\\ 0 & yScale & 0 & 0\\ 0 & 0 & -\frac{zFar+zNear}{zFar - zNear} & -\frac{2 \cdot zNear \cdot zFar}{zFar - zNear} \\ 0 & 0 & -1 & 0 \end{bmatrix}\cdot \)

Where \(yScale = \cot (\frac{fovy}{2})\) and \(xScale = \frac{f}{aspect}\).

See the CreateProjectionMatrix function in the file Utils.c for implementation details.

Drawing a Cube

Now that you have a basic knowledge of transformations, let's apply them and draw a rotating cube to the screen. Once again, the program that we created in chapter one serves as the basis for this exercise, so copy chapter.1.c (or chapter.1.3.c if you're getting it from the source code repository) to a new file called chapter.4.1.c.

First, remove all of the #include directives from the file, and replace them with a single #include to Utils.h:

As with each chapter, update WINDOW_TITLE_PREFIX to reflect the current chapter.

After the FrameCount variable, declare the following block of variables:

Underneath that, add the following matrices:

Right below that, add the following variable declarations:

Underneath the declaration of the IdleFunction function, insert the following new function declarations:

Inside of the Initialize function definition, make the following function call right above the function call to glClearColor:

Then, right underneath the call to glClearColor, insert the following lines:

Inside of the InitWindow function definition, right after the function call to glutTimerFunc, place the following line:

Next, inside of the ResizeFunction function definition, underneath the call to glViewport, insert the following lines:

In the RenderFunction function definition, right after the call to glClear, place the following function call:

We'll be entering the following function definition piece by piece in logical steps. First, create the following empty function definition:

At the first line of the function, insert the cube's vertex definitions:

Right after that, insert the cube's index definitions:

After that, place the following shader-program creation code:

Immediately underneath that, place the following shader loading and attaching code:

After that, insert the code to retrieve the shader uniforms:

Right below that, insert the following buffer generation code:

Insert the following VAO generation and binding code after that:

After that, enable the following vertex attribute locations:

Insert the following VBO binding, data uploading, and vertex attribute descriptions after that:

For the final lines of the function, insert the IBO binding and uploading code:

Immediately after the CreateCube function definition, insert the following new function definition:

The last function we'll define draws the cube to the screen. Insert the following empty function definition immediately after the DestroyCube function definition:

At the first line of the function, insert the following lines used for time-based rotations:

After that, insert the following matrix transformations:

Immediately after that, insert the following shader related function calls:

Finally, insert the last lines of this function used for drawing purposes:

Next, create a text file called SimpleShader.vertex.glsl, and insert the following lines:

Lastly, create another text file called SimpleShader.fragment.glsl with the following containing the following lines:

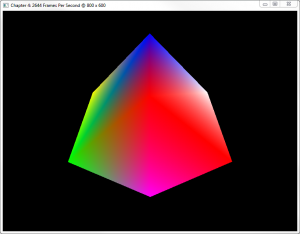
After you compile your program, make sure that these GLSL files are in the same directory as your executable before your run the executable. When you do, the output should show a spinning cube on your screen, similar to the following screenshot:

Chapter 4 Output

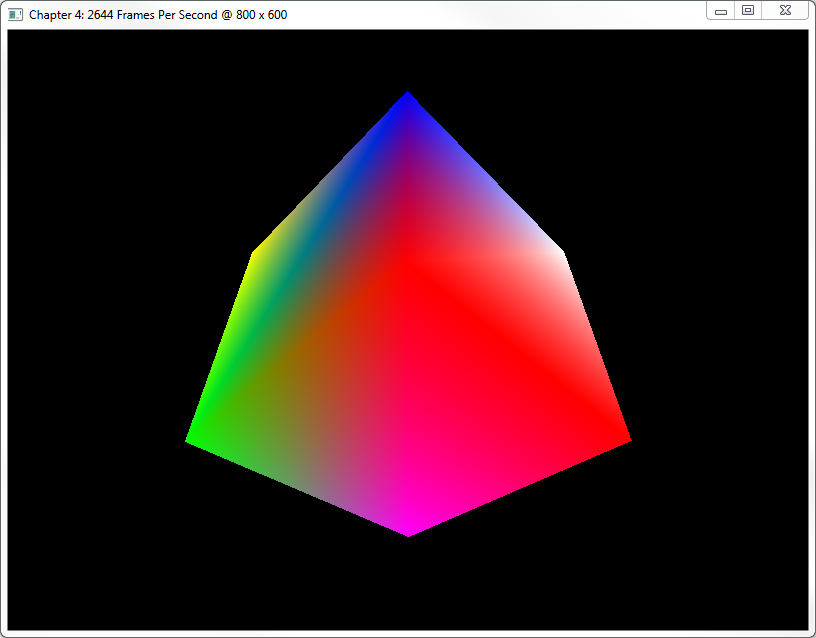
Step-By-Step

There are many changes from the previous chapters in this chapter, so let's look at what just happened. The first thing we did is the same we do for each chapter, which is to include files and change the window title's prefix. However, in this chapter, we replaced all of the #includes with a single include to Utils.h.

Before we continue describing the code, let's introduce a few new concepts.

GLSL Uniforms

In the previous chapters, we've learned that we can declare variables in our GLSL shaders, but haven't actually imported any data besides our usual vertex information. In this chapter, we need a way to transport our matrices to the vertex shader, and we do so by using so-called uniforms.

Uniforms are global variables stored inside of the shader program, changeable at any time during the lifecycle of the shader program. Once a uniform is set, it doesn't change and remains set until another value is set or the program ends.

Uniforms can be any basic GLSL data type, in our case they are of type mat4, which represents 4x4 matrices. In a future chapter on shaders, we'll discuss more GLSL data types.

Retrieving Uniform Locations

Each uniform has a specific location, and after a GLSL shader program links, these locations become available to OpenGL. The locations are accessible through their names by calling the OpenGL function glGetUniformLocation:

The program parameter takes in the shader program's identifier as generated by the call to glCreateProgram
The name parameter takes in the name of the uniform variable as defined in the GLSL source code as a regular character string

The function returns the integer uniform location, which we store in our ModelMatrixUniformLocation, ViewMatrixUniformLocation, and ProjectionMatrixUniformLocation variables.

Setting Uniform Data

Once we have these locations, we can start uploading our matrices to the GPU. To do so, there are many glUniform functions, one for each basic GLSL data type. The one we use in our program is glUniformMatrix4fv, which allows us to upload a 4x4 floating-point matrix:

The location parameter takes in the location of the uniform as queried by the glGetUniformLocation function described above
The count parameter takes in the number of matrices passed into this function: 1 for a single matrix, greater than1 for an array of matrices
The transpose parameter takes in GL_FALSE if the matrix is in column major order (as in our case), and GL_TRUE if the matrix is in row major order and requires transposing by OpenGL
The value parameter takes in a pointer to the location in memory of the first element of the array to upload to the GPU

Matrices in OpenGL

We represent a matrix as an array of sixteen floating-point numbers. The identity matrix in C looks like the following piece of code:

If we lay it out in a bit more readable format (as in Utils.h), we can see the layout of the matrix:

The matrix's column vectors occupy contiguous memory, meaning that the x-column vector occupies indices 0 through 3; the y-column vector occupies indices 4 through 7, and so on.

In our programs, we'll be using a structure containing one of these arrays named Matrix, defined in the file Utils.h. All of our helper functions operate on this structure, not a raw array of floating point numbers.

In this program, we store our matrices in three global variables named ModelMatrix for the cube's local transformations, ViewMatrix for the camera/eye transformation, and ProjectionMatrix for our perspective projection transformation. These variables have the exact same names as the uniform variables in our vertex shader, described further on in this chapter.

Step-By-Step Continued...

The next set of global variables that we added after our matrices and uniform locations, are a floating-point number named CubeRotation, and a clock_t variable named LastTime. We use both of these variables to rotate the cube in the DrawCube function, which we will describe a bit later on in the chapter.

We added a few more function declarations, and after that edited the Initialize function.

New Initialization Code (`Initialize`)

While much of the code in the Initialize function remained untouched, we added some crucial new function calls.

Depth Testing

Immediately after the call to glClearColor, we called the function glEnable, which allows us to enable certain OpenGL capabilities. The capability we wish to enable is the only parameter we pass to this function. To disable the capability, simply call glDisable with the same flag, which we do not use in our program.

The flag we pass into glEnable is GL_DEPTH_TEST, which allows OpenGL to compare the depth values of fragments after rasterization. Besides the GL_DEPTH_TEST capability enabled, OpenGL also needs to know exactly how to compare the fragments. We do this by a call to glDepthFunc, which defines when to store a fragment in the depth buffer, or when to discard by passing in one of the following enumerations:

GL_NEVER: a fragment never passes the depth test.
GL_LESS: a fragment passes when its depth value is less (closer to the camera) than the fragment currently stored in the depth buffer. We use this enumeration in our program.
GL_EQUAL: a fragment passes the depth test when its depth value is equal to the one currently stored in the depth buffer.
GL_LEQUAL: a fragment passes the depth test when its depth value is less or equal to the one currently stored in the depth buffer.
GL_GREATER: the opposite of GL_LESS.
GL_NOTEQUAL: the opposite of GL_EQUAL.
GL_GEQUAL: a fragment passes the depth test when its depth value is greater or equal to the one currently stored in the depth buffer.
GL_ALWAYS: the opposite of GL_NEVER.

OpenGL Error Checking

After the call to glDepthFunc, we call another new function is, namely our custom ExitOnGLError function. This function, as its name suggests, checks for an OpenGL error, and if one is present, immediately exits the program. A single parameter, error_message, is required that contains the error message to display to the user if the program exits erroneously.

Polygon Culling

This next concept is very important from this chapter onwards. Whereas in previous chapters we didn't care which way we constructed our vertices, with polygon culling, a method that reduces the amount of polygons to render, it becomes critical. For instance, if we didn't specify polygon culling in this chapter, rendering also occurs on the insides of the cube, even though they are not visible.

The first function call is once again glEnable, this time passing in the GL_CULL_FACE flag to enable the polygon capability on the graphics hardware.

The next function is glCullFace, which defines which face of the polygon to cull. We can cull either the front-face of the polygon by supplying the function with the GL_FRONT enumeration, the back-face of the polygon with GL_BACK, or both faces with GL_FRONT_AND_BACK. Yet, how do you determine which face is the front-face and which face is the back-face of a polygon?

The answer is by defining in which direction a polygon's vertices wind, either clockwise or counterclockwise. Vertex winding defines the path OpenGL takes to complete the polygon, starting at the first vertex, then the second vertex, and so on until the polygon is closed. We specify this direction with a call to glFrontFace, which defines the direction in which the vertices of a polygon wind. In our case, this is counterclockwise, specified by the GL_CCW enumeration, its opposite is GL_CW for clockwise winding vertices.

Matrix Initialization

After the OpenGL options are set, we initialize the matrices by setting them to the identity matrix. The view matrix, which describes the eye transformations, is translated two units into the negative z direction (backwards) so that the camera won't intersect the cube.

Creating the Cube (`CreateCube`)

We didn't encounter any new concepts in the CreateCube function; we still generate a bunch of buffers for vertex and index data and push them to the GPU. The only differences from the previous chapter are the retrieval of the shader uniforms described earlier and a new custom function named LoadShader.

Loading Shaders from Files

Previously, we hard-coded our GLSL shaders into our code as one giant constant string, from now on, we'll use the LoadShader function to load them from text files instead, its prototype looks like this:

The filename parameter takes in the filename of the GLSL shader to read
The shader_type parameter takes in the GLenum that we used to pass into glCreateShader, in this program we use GL_FRAGMENT_SHADER and GL_VERTEX_SHADER

The function reads the contents from the file, generates a shader identifier, passes the contents of the file into glShaderSource, and compiles the shader. The function returns the identifier generated by the call to glCreateShader.

Drawing the Cube (`DrawCube`)

The first section of the DrawCube function deals with generating a rotation angle based on the amount of time has passed. The rotation we use in this sample is 45 degrees per second, which we achieve by checking the amount of clock ticks passed since the last time the DrawCube function executed. The previous clock ticks are stored in the global variable LastTime, whereas the current ticks are stored in the local variable named Now.

The total rotation in degrees is stored in the global variable named CubeRotation. However, in order to use this rotation in OpenGL, we need to convert the degrees to radians, done through a function call to our custom function DegreesToRadians. This value is then stored in the local CubeAngle variable and used to apply rotational transformations to the model matrix by calling RotateAboutY, followed by a call to RotateAboutX.

Unlike in the previous chapters, we enable and disable the shader program as well as the VAO each draw call instead of just once to demonstrate how a scene with multiple objects is usually drawn. We'll introduce multiple objects to our scene in a future chapter, although there is nothing special about it, and by now, you should be able to work out how to do this from the information presented throughout the chapters.

Vertex Shader Changes

Besides changes to the C code, there were also some minor changes to the vertex shader from the previous chapter to the current one.

The first major change is the addition of the uniform variables described earlier in the chapter. In the GLSL source code, they look like this:

As mentioned earlier, the matrices in the shader have the exact same names as the ones in the source code. This is not a requirement, but simply to show the relationship between the two.

The final notable change to the vertex shader is the calculation of the final vertex position:

As you can see, the transformation for the vertex happens by multiplying the matrices together to form one transformation matrix (the multiplication between the parentheses), and multiplying in_Position with it to obtain the coordinates passed on to OpenGL.

Conclusion

In this chapter, we rendered our first three-dimensional geometry onto the screen and learned about the basic transformations used in computer graphics.

If you're fuzzy on matrix mathematics or linear algebra in general, here are a few resources to get you up to speed since the topic is too broad to handle on this site:

The Khan Academy, tons of great video tutorials on mathematics.
The matrix and quaternions FAQ
Any search result page on Google for "linear algebra," "matrix math," or "3D math" will do.

Until the next chapter is ready, try the following exercises:

Create a keyboard movable camera by transforming the ViewMatrix matrix through keyboard input (see chapter 3 for FreeGLUT keyboard input), copied to the GPU each time DrawCube executes.
Work out how to draw multiple cubes onto the screen.

You can find the source code for the samples in this chapter here.

OpenGLBook.com